A unit of telecom traffic
An Erlang is a unit of telecommunications traffic measurement. Strictly, an Erlang represents the continuous use of one voice path. In practice, it is used to describe the total traffic volume of one hour.
For example, if a group of user made 30 calls in one hour and each call had an average call duration of 5 minutes, then the traffic figure is worked out as follows:
| Minutes of traffic in the hour | = | number of calls x duration |
| Minutes of traffic in the hour | = | 30 x 5 |
| Minutes of traffic in the hour | = | 150 |
| Hours of traffic in the hour | = | 150 / 60 |
| Hours of traffic in the hour | = | 2.5 |
| Traffic figure | = | 2.5 Erlangs |
As a telecommunications network planner, traffic measurements or estimates are essential if you are to successfully design your network topology and establish the necessary trunk group sizes. They can be used to work out how many lines you require between your telephone system and a central office, or between multiple network locations.
Erlang traffic models
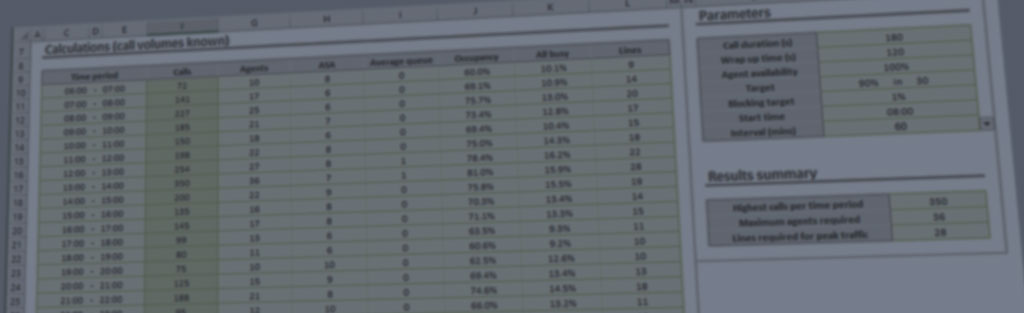
Several traffic models exist that share their name with the Erlang unit of traffic. They are formulae that can be used to estimate the number of lines you require in a network or to a central office (telephone exchange). A formula was also established to model queuing situations, and lends itself well to estimating the agent staffing requirements of call centers.
The main Erlang traffic model are listed below, with links to our free online Erlang calculators:
- Erlang B
The most commonly used traffic model, it estimates how many lines you need if you know the traffic figure (in Erlangs) during your busiest hour. - Extended Erlang B
This model is similar, but takes into account that a percentage of calls are immediately repeated if they encounter blocking (a busy signal). The retry percentage can be specified. - Erlang C
This traffic model assumes that all blocked calls stay in the system until they can be handled. You can apply it to the design of call center staffing arrangements where calls enter a queue if they are not answered immediately.
We are the trusted supplier of industry-standard Erlang software tools to tens of thousands of companies in 125 countries.
Applying the traffic models
You can use the Erlang B traffic model to work out how many lines your system needs, and we describe this in detail in this technical paper.
Our Call Center Design paper describes how to use the Erlang C traffic model to estimate how many call handlers you need at your help desk or call center.
Frequently asked questions
Erlang B is a formula that helps you estimate how many telephone trunks you need if you know the volume of calls that it will be expected to handle. You can perform Erlang B calculations on your desktop or in spreadsheets.
In the last century, engineers used printed tables published in huge traffic engineering books to look up how many lines they needed. Now, these calculations can be performed using Erlang add-ins for Excel or standalone Erlang desktop applications.
An Erlang calculator is a twentieth-century replacement for Erlang tables, used by telephone engineers to work out how many lines or operators they need. We’ve been providing them since 1996.
Erlang C is a formula for modelling systems involving queuing. You can use it to estimate how many call center agents you need to keep your call queue down to manageable levels.
Excel does not include native Erlang formulae, but you can bring Erlang B and Erlang C into your spreadsheets with an Excel add-in.
Erlang B and C have been used since the first half of the twentieth century and have endured because of their accuracy. Nevertheless, you should use them with caution as they make certain assumptions, such as the random nature of call arrivals.
A.K. Erlang – a tribute

Agner Krarup Erlang was born in 1878 in Lønborg, Denmark. He was a pioneer in the study of telecommunications traffic and, through his studies, proposed a formula to calculate the fraction of callers served by a village exchange that would have to wait when attempting to place a call to someone outside the village.
In 1909, he published his first work: The Theory of Probabilities and Telephone Conversations. He gained worldwide recognition for his work and his formula was accepted for use by the General Post Office in the UK.
He never married, and worked for the Copenhagen Telephone Company for twenty years, until his death in 1929. During the 1940s, the Erlang became the accepted unit of telecom traffic measurement, and his formula is still used today in the design of modern networks.


Superb explanation, really helpful. Thank you.
Thank you so much
You’re welcome
I need to the exact formula of Erlang B please.
Thank you so much!
I looked this up to find out why software written for amateur radio (Automatic Position Reporting System, APRS) would have a whole set of functions written to support this as a metric. I needed to know WTF this was, and why the developer went to all that trouble … and if I should care. Turns out I do actually.
Hey Mark, what’s the connection then between Erlangs and APRS? And when you say the developer, do you mean of erlang.com (me) or APRS?
BTW, your QRZ.com profile makes great reading. I’m also a radio amateur.